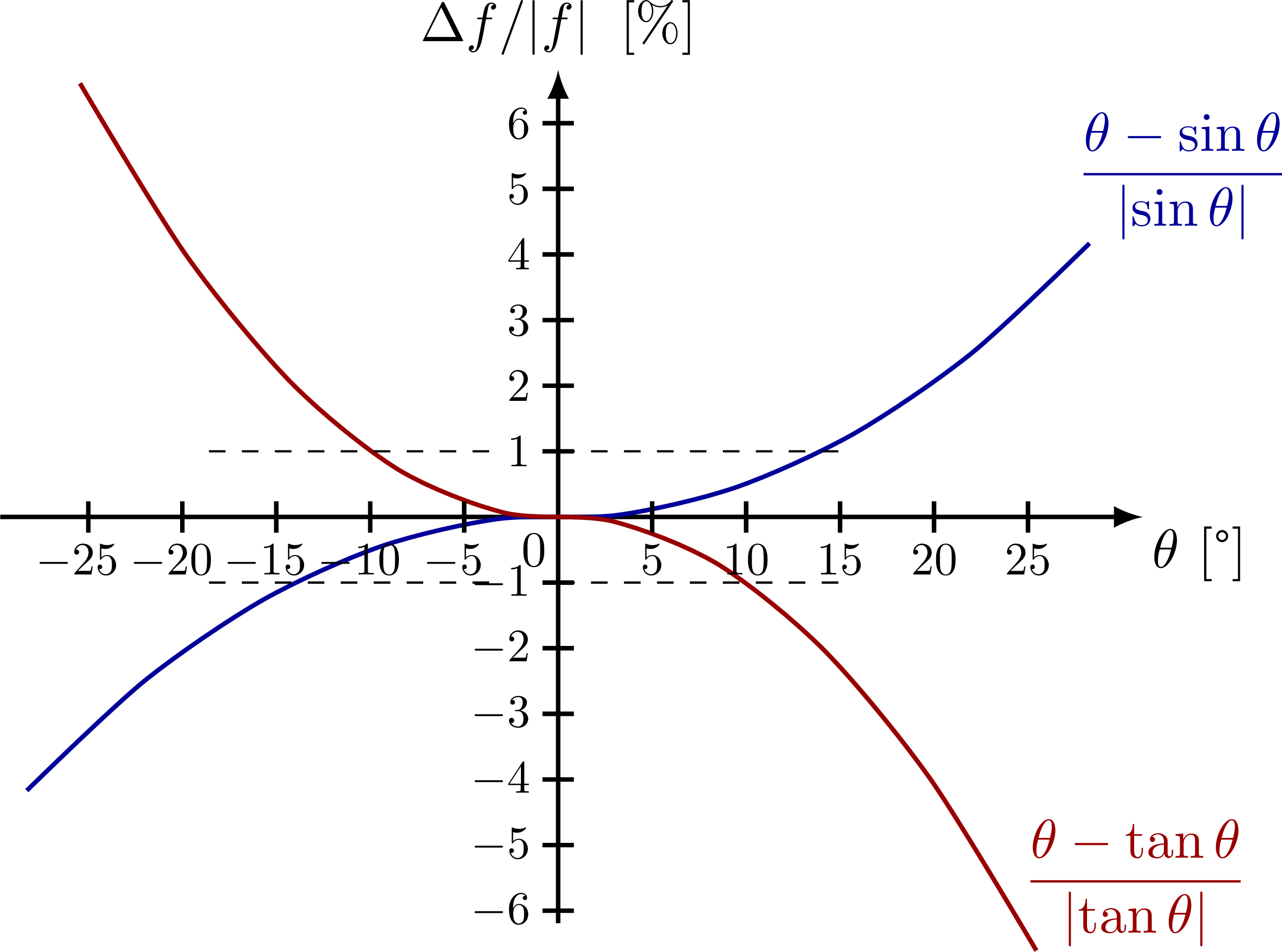
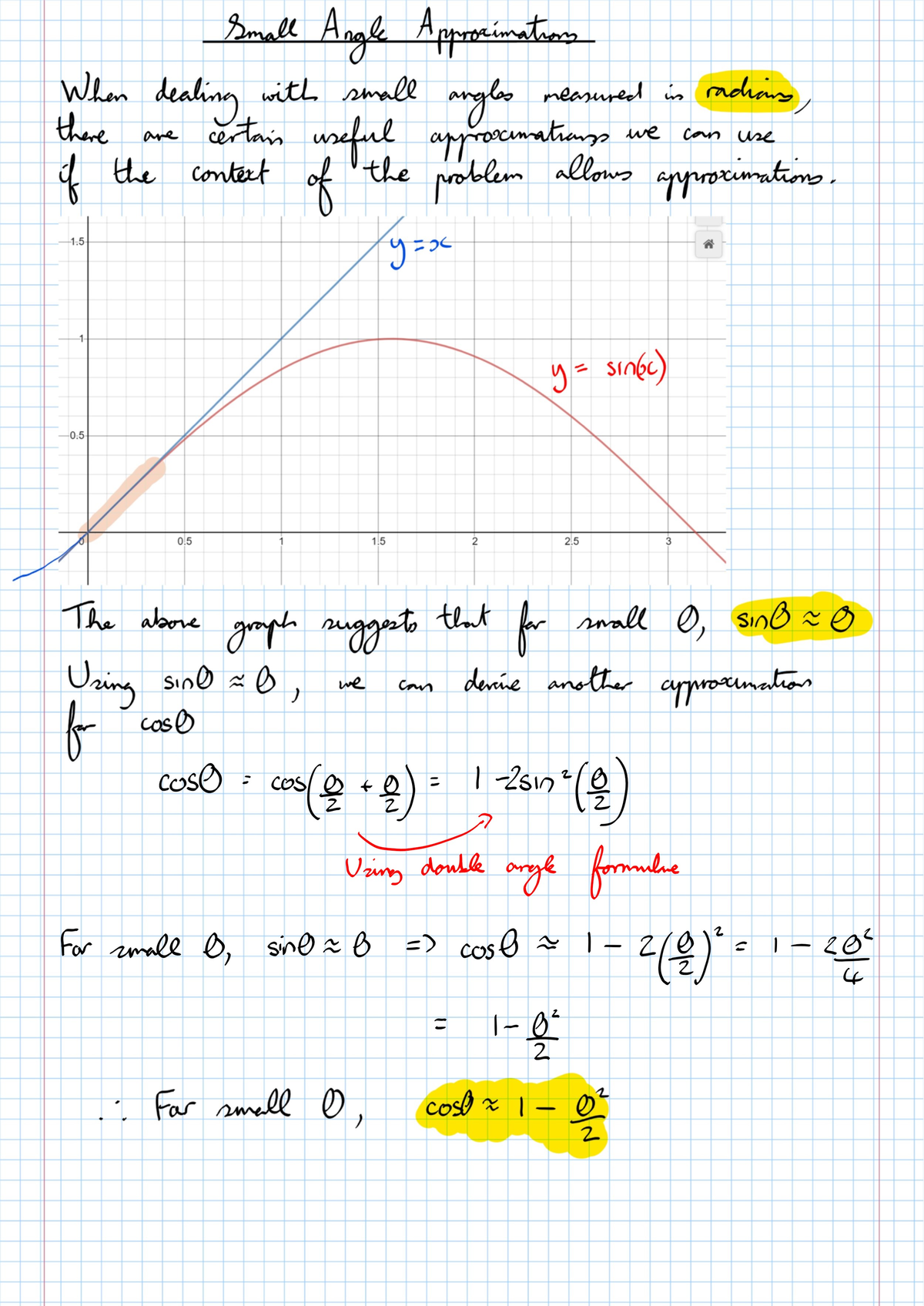
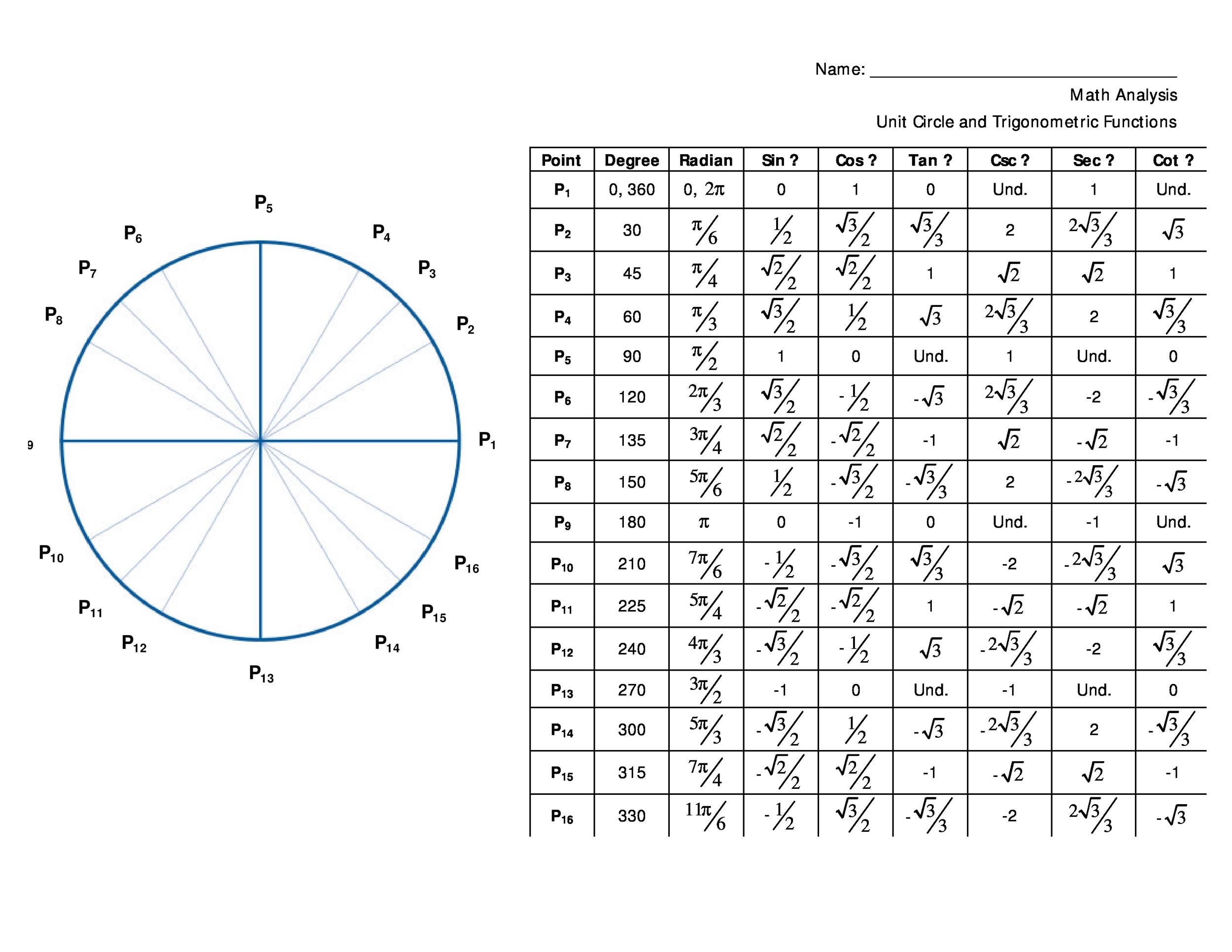
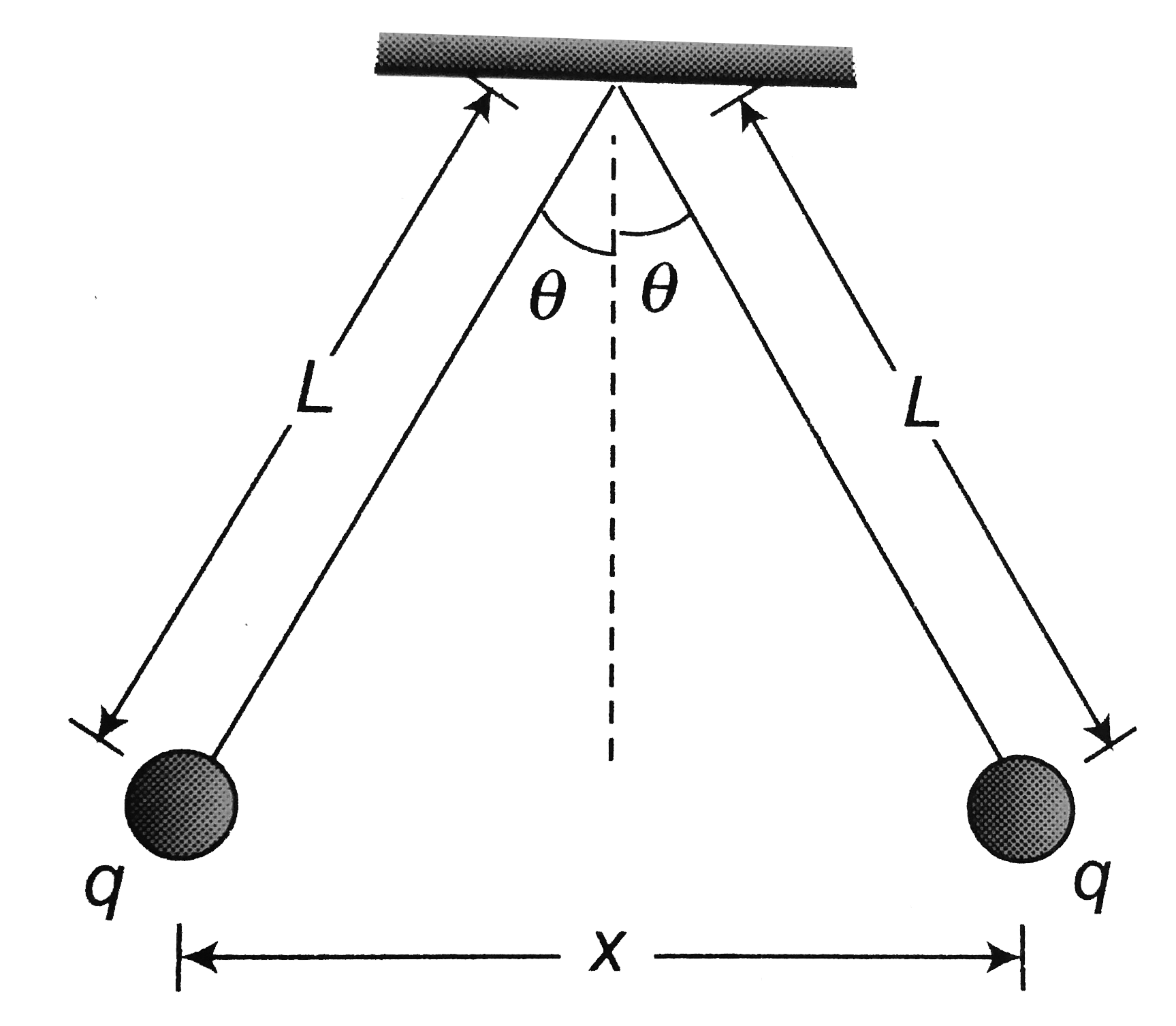
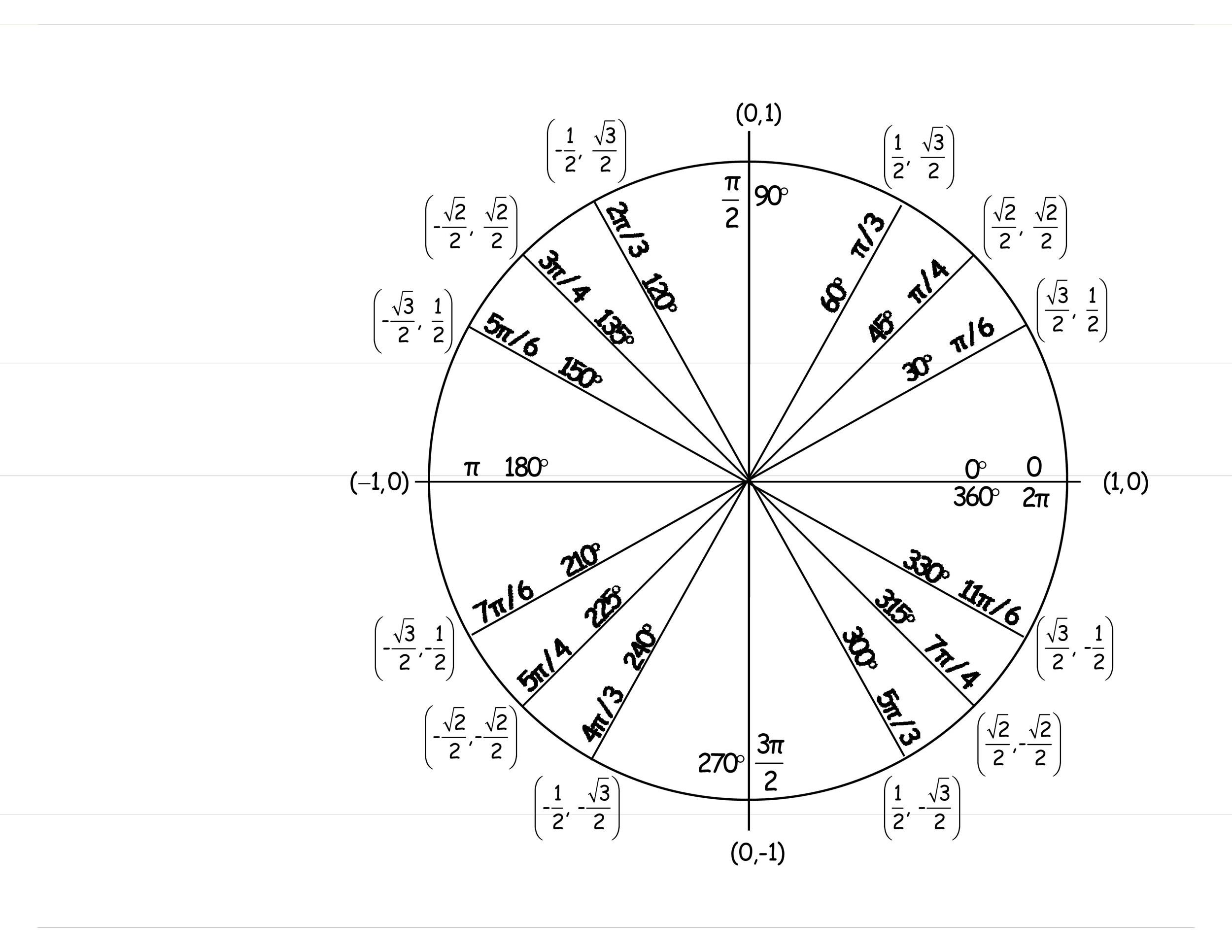
Webwe can find approximations of the trigonometric functions for small angles measured in radians by considering their graphs near input values of 𝑥 = 0. Let’s start with 𝑦 = 𝑥 s i n and compare it to line 𝑦 = 𝑥. When the angle θ (in radians) is small we can use these approximations for sine, cosine and tangent: Sin θ ≈ θ. Cos θ ≈ 1 − θ2 2. Tan θ ≈ θ. If we are very daring we can use cos θ ≈ 1. Webrevision notes on 5. 4. 3 small angle approximations for the edexcel a level maths: Pure syllabus, written by the maths experts at save my exams. Webwhen the angle is small, the approximation reads $\sin \theta \approx \theta$, you can try this simulation below to verify the relation. Click try it to display the value of each element in the form. The angles are in radians, so :2 = :2 radians 11:4. (multiply by 180= to convert from radians to degrees, and by =180 to convert from degrees to radians. ) continuity of sin x at x = 0 tells us sin x ! Sin 0 = 0 as x !
Related Posts
Recent Post
- Ri Milesplit
- Textadventures Tiny
- Kevin Lapointe Pasco County
- Best Dispensary In Niles Michigan
- Saginaw River Cam
- Osbi Facebook
- The Peach Cobbler Factory Middletown Photos
- Doordash Dark Mode
- House For Rent Office
- Heartland Lyndy
- Apple Card Credit Limit Increase Myfico
- Jos Hours Osu
- Kia Optima Forum
- You Haul Storage
- Florida Lottery Claim Office
Trending Keywords
Recent Search
- Airbnb Bartow
- Stewart Hotel New York Trip Advisor
- Henrico Arrest
- Nelson County Busted
- Channel 22 Dayton
- Recent Obituaries In The Pittsburgh Post Gazette
- Justin Williams Crystal Ball
- Identogo William Penn Highway Easton Pa
- Stats Minor Ucla
- Budweiser Rebate Mailing Address
- Car Rental Near Utica Ny
- Bx36 Bus Route Map
- Saginaw River Mouth Webcam
- Groce Funeral Home Asheville Nc Obituaries
- Hardees Starting Pay